Optimasi merupakan salah satu kelompok masalah yang menjadi fokus penerapan ilmu komputer dalam kehidupan sehari-hari. Menemukan rute terpendek pada peta, menjadwalkan penerbangan, mengatur rute pengiriman paket jasa ekspedisi, menentukan persediaan barang di gudang untuk antisipasi kebahbisan stok, merupakan beberapa contoh masalah optimasi yang sering kita jumpai.
Karena aplikasi dari konsep optimasi ini sangat vital terhadap efisiensi dan keberlanjutan proses bisnis dan riset, maka kita khususnya mahasiswa dan peneliti ilmu komputer wajib mengetahui bagaimana konsep optimasi ini dapat kita manfaatkan untuk menyelesaikan berbagai masalah di dunia nyata.

Optimasi sendiri merupakan salah satu cabang dari matematika dan pastinya akan menggunakan kalkulus. Nah teman-teman yang mungkin sudah lupa tentang limit, turunan, dan integral akan perlu mengingat kembali konsep-konsep tersebut karena akan sangat digunakan pada proses optimasi.
Pada artikel kali ini penulis ingin mencoba me-review mengenai optimasi mulai dari optimasi satu variabel, dua variabel, optimasi dengan kendala, dan metode numerik untuk menyelesaikan masalah optimasi.
Review Optimasi Satu Variabel📖
Pada optimasi analitik, jika diberikan fungsi $f(x)$ yang dapat diturunkan, $f’(x)$ dan $f’’(x)$ maka dapat ditentukan titik optimum (maksimum/minimum) lokal/global dari $f(x)$.
Turunan pertama $f’(x)$ menunjukkan gradien/kemiringan
- $f’(x) > 0$, kemiringan naik
- $f’(x) = 0$, titik kritis
- $f’(x) < 0$, kemiringan turun
Turunan kedua $f’’(x)$ menunjukkan jenis titik ekstrem
- $f’’(x) > 0$, titik minimum
- $f’’(x) = 0$, titik balik/inflection point
- $f’’(x) < 0$, titik maksimum
Contoh 1
Diberikan fungsi $f(x) = x^2-4x+1$, tentukan titik optimumnya!
Jawab
Tentukan turunan pertama dari $f(x)$,
$$ f'(x) = 2x-4 $$Tentukan nilai $x$ dengan mencari $f’(x)=0$,
$$ \begin{aligned} f'(x) &= 0 \\\ 2x-4 &= 0 \\\ x &= 2 \end{aligned} $$Didapatkan nilai kritis $x=2$. Untuk menentukan jenis titik kritis tersebut, cari $f’’(x)$,
$$ f''(x) = 2 $$Karena $f’’(x) = 2 > 0$, berarti titik $(2, -3)$ merupakan titik minimum.
Tips💡 Klik logo Desmos untuk mencoba grafik versi interaktif
Nah sudah cukup teringat kan dengan metode optimasi? Sekarang bagaimana jika kita ingin melakukan optimasi dua atau lebih variabel?
Turunan Parsial dan Turunan Berarah🎢
Jika kita ingin melakukan optimasi pada fungsi yang memiliki dua atau lebih variabel, maka kita perlu menentukan turunan parsial untuk masing-masing variabel. Pada kasus ini kita akan fokus pada optimasi fungsi dua variabel.
Untuk menentukan turunan parsial kita bisa menggunakan definisi limit, jika $z=f(x,y)$, maka:
$$ \begin{aligned} f_x(x_0, y_0) &= \lim_{h \to 0} \frac{f(x_0+h,y_0)-f(x_0,y_0)}{h} \\\ f_y(x_0, y_0) &= \lim_{h \to 0} \frac{f(x_0,y_0+h)-f(x_0,y_0)}{h} \end{aligned} $$menyatakan laju perubahan $z$ pada arah $x$ dan $y$.
Kemudian bagaimana cara kita menentukan titik kritis dari fungsi yang memiliki dua variabel? Solusinya adalah kita perlu menentukan solusi persamaan dari turunan parsial terhadap masing-masing variabel.
$$ \begin{aligned} f_x(x,y) &= \frac{\mathrm{d} f(x,y)}{\mathrm{d}x} = 0 \\\ f_y(x,y) &= \frac{\mathrm{d} f(x,y)}{\mathrm{d}y} = 0 \end{aligned} $$Berdasarkan turunan pertama tadi, kita bisa membentuk vektor arah/gradien/kemiringan atau disebut juga Jacobian pada titik $(x,y)$ yang ditunjukkan oleh nilai:
$$ \nabla f(x,y) = \begin{bmatrix} f_x(x,y) & f_y(x,y) \end{bmatrix} $$Sama seperti pada uji titik kritis pada optimasi satu variabel, kita juga perlu melakukan identifikasi jenis titik kritis, pada kasus ini, kita akan menggunakan matriks turunan kedua atau matriks Hessian.
$$ \mathbf{H} = \begin{bmatrix} f_{xx} & f_{xy} \\\ f_{xy} & f_{yy} \end{bmatrix} $$Misalkan turunan parsial kedua $f$ kontinu dengan pusat $(a,b)$, dan misalkan $f_x(a,b)=0$ dan $f_y(a,b)=0$, maka identifikasi jenis titik kritis dapat dilakukan dengan cara menentukan determinan dari matriks Hessian,
$$ D = f_{xx}f_{yy} - (f_{xy})^2 $$- Jika $D>0$ dan $f_{xx}(a,b)>0$, maka $f(a,b)$ adalah minimum lokal
- Jika $D>0$ dan $f_{xx}(a,b)<0$, maka $f(a,b)$ adalah maksimum lokal
- Jika $D<0$, maka $f(a,b)$ bukan maksimum atau minimum lokal (titik pelana)
- Jika $D=0$, berarti pengujian tidak memberikan informasi
Contoh 2
Diberikan fungsi $f(x,y) = 3x^3+y^2-9x+4y$, tentukan titik-titik optimumnya!
Jawab
Tentukan turunan parsial order pertama dari $f(x,y)$,
$$ \begin{aligned} f_x(x,y) &= 9x^2-9 = 0 \\\ f_y(x,y) &= 2y+4 = 0 \end{aligned} $$Dengan mencari faktor dari kedua turunan di atas, didapatkan dua titik yaitu (1, -2) dan (-1, -2) sebagai titik kritis. Tahap selanjutnya adalah mengidentifikasi jenis titik kritis tersebut dengan cara menghitung determinan dari matriks Hessian-nya.
Tahap selanjutnya adalah menghitung turunan kedua,
$$ \begin{aligned} f_{xx} &= 18x \\\ f_{xy} &= 0 \\\ f_{yy} &= 2 \end{aligned} $$Menentukan Jenis Titik (1, -2)
$$ \begin{aligned} f_{xx} (1,-2) &= 18 \\\ f_{xy} (1,-2) &= 0 \\\ f_{yy} (1,-2) &= 2 \\\ D &= (18)(2) - (0)^2 = 36 \end{aligned} $$Karena titik (1, -2) memiliki nilai $D=36>0$ dan $f_{xx}=18>0$, berarti titik ini adalah titik minimum.
Menentukan Jenis Titik (-1, -2)
$$ \begin{aligned} f_{xx} (-1,-2) &= -18 \\\ f_{xy} (-1,-2) &= 0 \\\ f_{yy} (-1,-2) &= 2 \\\ D &= (-18)(2) - (0)^2 = -36 \end{aligned} $$Karena titik (-1, -2) memiliki nilai $D=-36<0$, berarti titik ini adalah titik pelana.
Dengan mensubstitusikan titik (1, -2) ke dalam $f(x,y)$, didapatkan titik $(x,y,z)=(1,-2,-10)$ yang merupakan minimum lokal dari fungsi $f(x,y)$.
Optimasi dengan Kendala🚩
Sampai di sini kita sudah belajar mengenai optimasi fungsi tanpa kendala yang berarti kita tidak memiliki constraint atau batasan untuk menentukan titik optimum. Tetapi, sering kali kita membutuhkan proses optimasi yang memiliki kendala, misalnya mengoptimalkan produksi berdasarkan jumlah karyawan dan bahan baku. Tentunya kita tidak bisa sembarangan menentukan nilai optimum karena ada keterbatasan sumber daya tadi.
Untuk menyelesaikan optimasi dengan kendala, kita bisa menggunakan pendekatan menggunakan pengganda Lagrange atau Lagrange multiplier. Secara umum, Langrangian didefinisikan
$$ {\mathcal {L}}(x,\lambda )\equiv f(x) + \lambda \cdot g(x) $$untuk fungsi $f(x)$, $g(x)$; $\lambda$ disebut sebagai pengganda Lagrange. Dengan menggunakan konsep Jacobian pada metode optimasi sebelumnya, untuk mengoptimalkan fungsi dengan kendala, kita bisa formulasikan:
$$ \begin{aligned} \nabla f &= \lambda \nabla g \\\ \begin{bmatrix} f_x & f_y \end{bmatrix} &= \lambda \begin{bmatrix} g_x & g_y \end{bmatrix} \end{aligned} $$Selama nilai $\lambda$ terdefinisi, kita bisa mendapatkan solusi optimum untuk fungsi yang memenuhi kendala atau constraint.
Contoh 3
Diberikan fungsi $f(x,y) = 5x-3y$, tentukan titik-titik optimumnya dengan kendala $x^2+y^2=136$.
Jawab
Tahap pertama adalah menentukan nilai $x$ dan $y$ untuk menentukan nilai $\lambda$
$$ \begin{aligned} f_x = \lambda g_x &\rightarrow 5=\lambda 2x \\\ &\rightarrow x=\frac{5}{2}\lambda \end{aligned} \qquad \begin{aligned} f_y = \lambda g_y &\rightarrow -3=\lambda 2y \\\ &\rightarrow y=-\frac{3}{2}\lambda \end{aligned} $$selanjutnya substitusi nilai $x$ dan $y$ ke fungsi $g(x,y)$
$$ \begin{aligned} x^2+y^2 &= 136 \\\ \frac{25}{4\lambda^2} + \frac{9}{4\lambda^2} &= 136 \\\ \lambda^2 &= \frac{1}{16} \\\ \lambda &\rightarrow \pm \frac{1}{4} \end{aligned} $$Setelah kita mengetahui nilai $\lambda = \pm \frac{1}{4}$, kita bisa substitusikan kembali nilai ini ke $x$ dan $y$ di tahap pertama.
$$ \begin{aligned} x &= \frac{5}{2}\lambda \rightarrow \frac{5}{2(\frac{1}{4})} = 10 \\\ y &= -\frac{3}{2}\lambda \rightarrow -\frac{3}{2(\frac{1}{4})} = -6 \\\ &\rightarrow (10, -6) \end{aligned} \qquad \begin{aligned} x &= \frac{5}{2}\lambda \rightarrow \frac{5}{2(-\frac{1}{4})} = -10 \\\ y &= -\frac{3}{2}\lambda \rightarrow -\frac{3}{2(-\frac{1}{4})} = 6 \\\ &\rightarrow (-10, 6) \end{aligned} $$Sekarang kita sudah mendapatkan dua titik optimum yaitu (10,6) dan (-10,6). Tahap terakhir dari proses ini adalah menentukan jenis titik optimum tersebut yang mana kita bisa lakukan dengan cara yang sama seperti pada contoh soal sebelumnya.
The answer is left as an exercise for the reader😂
Nah sekarang kita sudah belajar bagaimana cara mencari titik optimum dua variabel menggunakan pendekatan pengganda Lagrange. Secara umum tahapan yang kita lakukan sama seperti optimasi tanpa kendala yaitu dengan memanfaatkan turunan pertama untuk mencari nilai kritis melalui pengganda Lagrange dan turunan kedua untuk mengidentifikasi jenis titik kritis.
Dengan menggunakan metode ini, kita bisa secara akurat menentukan titik-titik kritis tersebut dengan syarat, kita bisa menurunkan fungsi tersebut untuk mendapatkan matriks Jacobian dan Hessian-nya. Tapi bagaimana jika kita punya fungsi dengan banyak variabel?🤔
Metode Numerik🔟
Pada banyak kasus optimasi, sering kali tidak mungkin atau sangat sulit untuk dapat menghitung turunan fungsi yang akan dioptimasi (untuk menentukan matriks Jacobian dan Hessian). Maka dari itu, metode analitik menjadi tidak feasibel jika digunakan pada persamaan dengan banyak variabel.
Bagaimana solusinya?
Kita bisa menggunakan pendekatan metode numerik yaitu menggunakan aproksimasi sehingga tidak mendapatkan jawaban yang 100% tepat, tapi cukup mendekati jawaban yang terbaik.
Metode numerik juga menjadi alternatif yang diminati karena proses iterasi dapat dilakukan dengan cepat menggunakan komputer dan dapat menghasilkan jawaban yang sangat dekat dengan metode analitik. Pada metode numerik, kita akan melakukan iterasi untuk mencari jawaban terbaik, sehingga kita harus memiliki kondisi berhenti iterasi ketika dirasa sudah mendapatkan jawaban yang baik. Biasanya terdapat dua kondisi berhenti yang umum dipakai, yaitu jika (1) jawaban sudah konvergen/sedikit berubah atau (2) sudah mencapai batasan iterasi. Hal ini penting untuk kita tentukan di awal proses metode numerik karena kita tidak mungkin melakukan iterasi terus menerus.
Metode Gradient Descent🏔️
Gradient descent merupakan metode optimasi yang saat ini menjadi tulang punggung segala jenis model berbasis deep learning dan juga alasan kita sekarang bisa menikmati AI seperti ChatGPT, Bard, dan Copilot. Maka dari itu sangat penting untuk teman-teman khususnya yang mempelajari machine learning untuk mengetahui metode ini.
Ide utama dari metode gradient descent adalah mengikuti arah kecuraman (naik/turun) paling tinggi.

Bayangkan teman-teman sedang berada di puncak gunung dan ingin turun kembali ke jalan utama. Saat itu sudah sore hari dan kondisi berkabut sehingga teman-teman tidak bisa melihat arah mana yang akan menuju titik terendah, bagaimana cara kita untuk bisa turun dengan cepat dari gunung tersebut?
Kita bisa mengikuti jalur dengan kemiringan terbesar. Meskipun kita tidak bisa melihat ada di mana lokasi titik terendah, tapi dengan mengikuti kemiringan gunung pada akhirnya kita akan sampai pada titik terendah. Nah inilah konsep utama dari metode gradient descent.
Foto oleh: KSmrq (berlisensi GFDL) dari Wikimedia Commons
Tapi bagaimana jika kita ternyata menemukan kemiringan terbesar, tetapi ternyata kita malah berakhir di danau atau kawah (local minima/saddle point), bukan ke titik terendah yang menuju ke jalan utama (global minima)? Nah kondisi ini merupakan salah satu kekurangan dari metode gradient descent, jika kita salah melangkah, maka ada kemungkinan kita tidak akan mendapatkan nilai optimum terbaik.
Secara matematis, jika suatu fungsi $f(x)$ memiliki turunan pada titik $a$, maka $f(x)$ akan menurun paling cepat jika titik $a$ bergerak pada arah kemiringan negatif $-\nabla f(a)$.
$$ a_{i+1} = a_i - \gamma \nabla f(x) $$Konstanta $\gamma$ disebut step size atau learning rate, konstanta ini mengatur seberapa jauh setiap langkah yang diambil saat bergerak mengikuti gradien. Nilai ini sangat penting untuk kita pilih dengan baik karena jika kita salah memilih nilai $\gamma$, maka kita mungkin tidak akan bisa menemukan titik optimum.
Misalnya kita akan mengoptimasi fungsi $f(x) = x^2-4x+1$ dengan tebakan awal $x_0=6$ dan maksimum iterasi sebanyak 15 kali. Bagaimana hasil optimasinya menggunakan gradient descent?
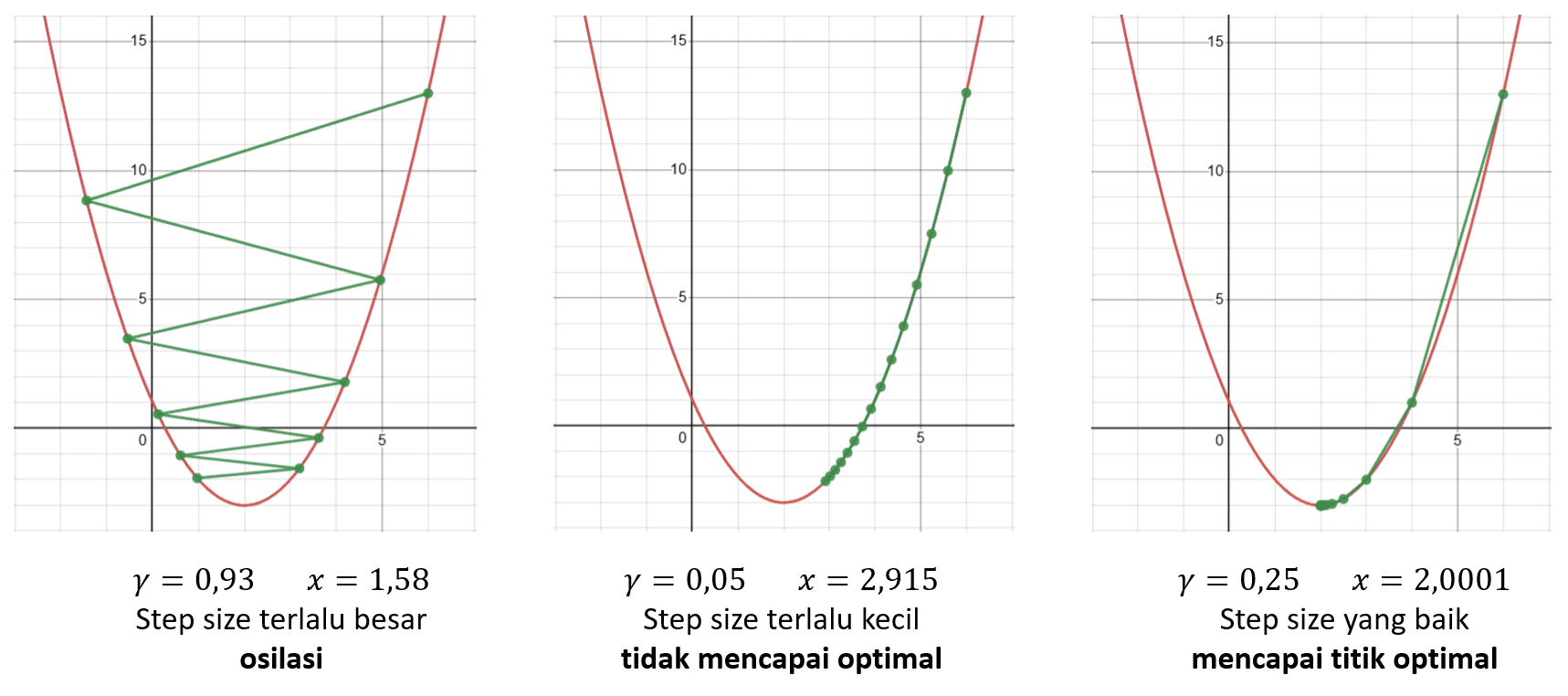
Gambar oleh penulis
Pada gambar di atas kita bisa lihat jika kita menggunakan nilai $\gamma$ yang terlalu besar, maka akan terjadi osilasi atau hasil optimasinya akan naik turun, hal yang sama juga terjadi jika kita menggunakan nilai $\gamma$ yang terlalu kecil, bukan terjadi osilasi tapi metode gradient descent tidak bisa mencapai titik optimal karena iterasinya sudah terhenti karena maksimum iterasi alias proses pergerakan titiknya terlalu lambat. Jika kita menggunakan nilai $\gamma$ yang optimal, maka kita akan bisa mencapai titik optimum yaitu $x \approx 2.0$.
Kemudian muncul pertanyaan, bagaimana cara menentukan nilai $\lambda$ yang optimal? Sayangnya pembahasan ini di luar artikel kali ini🥲 Tapi secara umum, teman-teman bisa menggunakan step size yang lazim digunakan yaitu 0,001; 0,01; dan 0,1. Selain itu, teman-teman bisa melakukan trial and error untuk melihat bagaimana hasil optimasinya apakah sudah baik atau belum.
Contoh 4
Diberikan fungsi $f(x) = x^2-4x+1$, step size sebesar 0.25 dan tebakan awal 6, tentukan titik optimumnya!
Jawab
Tentukan turunan pertama dari fungsi,
$$ f'(x) = 2x - 4 $$Lakukan iterasi,
$$ \begin{aligned} a_{i+1} &= a_i - \gamma (2x-4) \\\ a_1 &= 6 - (0.25)(2(6) - 4) = 4 \\\ a_2 &= 4 - (0.25)(2(4) - 4) = 3 \\\ a_3 &= 3 - (0.25)(2(3) - 4) = 2.5 \\\ a_4 &= 2.5 - (0.25)(2(2.5) - 4) = 2.25 \\\ a_5 &= 2.25 - (0.25)(2(2.25) - 4) = 2.125 \\\ a_6 &= 2.125 - (0.25)(2(2.125) - 4) = 2.0625 \\\ a_7 &= 2.0625 - (0.25)(2(2.0625) - 4) = 2.03125 \end{aligned} $$Pada iterasi ketujuh kita mendapatkan nilai $x \approx 2.0$, jika kita teruskan proses iterasi maka kita akan mencapai nilai tepat $x = 2$ setelah 28 iterasi. Nah sekarang terlihat kan kenapa nilai $\gamma$ dan banyaknya iterasi sangat berpengaruh apakah titik optimum akan ditemukan atau tidak.
Untuk mempermudah teman-teman memahami konsep gradient descent, teman-teman bisa buka aplikasi Desmos di atas untuk melihat bagaimana proses iterasi dilakukan dan teman-teman juga bisa mencoba fungsi lain di aplikasi Desmos lo!
Metode Newton🌎
Ide dari metode Newton adalah menggunakan turunan kedua untuk mencari langkah tercepat menuju minimum sehingga skema iterasinya adalah:
$$ x_{i+1} = x_i - \frac{f'(x_i)}{f''(x_i)} $$Jika fungsi yang akan dioptimalkan memiliki dua atau lebih variabel, nilai turunan kedua diganti dengan matriks Hessian.
$$ \mathbf{H} = \begin{bmatrix} % row 1 \frac{\partial^2f}{\partial x_1^2} & \frac{\partial^2f}{\partial x_1 \partial x_2} & \dots & \frac{\partial^2f}{\partial x_1 \partial x_n} \\\ % row 2 \frac{\partial^2f}{\partial x_2 \partial x_1} & \frac{\partial^2f}{\partial x_2^2} & \dots & \frac{\partial^2f}{\partial x_2 \partial x_n} \\\ % row 3 \vdots & \vdots & \ddots & \vdots \\\ % row 4 \frac{\partial^2f}{\partial x_n x_1} & \frac{\partial^2f}{\partial x_n \partial x_2} & \dots & \frac{\partial^2f}{\partial x^2_n} \end{bmatrix} $$sehingga formula iterasinya adalah:
$$ \begin{aligned} x_{i+1} &= x_i - \frac{\nabla f(x_i)}{H(x_i)} \\\ &= x_i - [H(x_i)]^{-1} \nabla f(x_i) \end{aligned} $$Catatan: pada literatur lain teman-teman mungkin menjumpai metode Newton-Raphson yang menggunakan fungsi asli dan turunan pertama tanpa turunan kedua dengan formulasi $x_{i+1} = x_i - \frac{f(x_i)}{f’(x_i)}$
Contoh 5
Diberikan fungsi $f(x) = x^2-4x+1$ dan tebakan awal $x_0=10$, tentukan titik optimumnya! (max 100 iterasi)
Jawab
Menentukan turunan pertama dan kedua,
$$ \begin{aligned} f'(x) &= 2x - 4 \\\ f''(x) &= 2 \end{aligned} $$Melakukan iterasi,
$$ \begin{aligned} x_{i+1} &= x_i - \frac{f'(x_i)}{f''(x_i)} = x_i - \frac{2x_i-4}{2} \\\ x_1 &= 10 - \frac{2(10)-4}{2} = 6 \\\ x_2 &= 6 - \frac{2(6)-4}{2} = 2 \\\ x_3 &= 2 - \frac{2(2)-4}{2} = 2 \\\ x_4 &= 2 - \frac{2(2)-4}{2} = 2 \qquad \text{(stop)} \end{aligned} $$Ternyata setelah empat iterasi saja kita sudah menemukan bahwa persamaan ini memiliki nilai optimum 2, sama seperti pada Contoh 1.
Trivia: penggunaan metode Newton pada persamaan kuadratik memiliki ciri khas khusus yaitu kita dipastikan akan mendapatkan nilai optimum setelah dua iterasi saja!😮
Penutup
Optimasi merupakan salah satu studi yang sangat penting dan banyak pengaplikasiannya di ilmu komputer dan menjadi tulang punggung teknologi AI yang saat ini kita sering gunakan seperti ChatGPT, Bard, dan lainnya.
Pada artikel kali ini kita sudah mempelajari bagaimana cara melakukan optimasi satu variabel, dua variabel, optimasi dengan kendala, dan pendekatan metode numerik untuk optimasi. Artikel ini mungkin sedikit berbeda dari artikel yang biasanya penulis bawakan mengenai teknologi, tetapi kali ini mengenai matematika🥲.
Menurut penulis artikel ini penting karena (1) penulis baru selesai UAS dan ingin me-review kembali materi UAS🤣 dan (2) konsep seperti gradient descent sangat penting apalagi jika penulis nantinya akan membahas mengenai deep learning dan neural network.
Yap, penulis sudah memiliki beberapa draf artikel bertopik neural network, scraping, dan lainnya yang akan di rilis nanti dan artikel ini adalah fondasi untuk artikel-artikel yang akan datang.
Stay tuned ya semua!
Referensi📚
- IPB. 2023. Matematika Statistika Komputasi (KOM501) Pertemuan 12 Turunan Parsial, Gradien, Titik Kritis Fungsi.
- IPB. 2023. Matematika Statistika Komputasi (KOM501) Pertemuan 13 Maksimum dan Minimum Fungsi.
- IPB. 2023. Matematika Statistika Komputasi (KOM501) Pertemuan 14 Teknik Optimasi.