Artificial intelligence (AI) saat ini sudah menjadi bagian dari kehidupan kita. Siapa yang tidak kenal ChatGPT? Artificial intelligence terobosan OpenAI ini mengubah kebiasaan kita dan meningkatkan produktivitas kita melalui otomasi dan pencarian informasi sangat mudah, ditambah dengan antarmuka berupa chatting, membuat interaksi kita lebih natural dan bisa memberikan kita berbagai informasi yang dibutuhkan dalam sekejap mata.
Terobosan AI ini tentunya berdasarkan pada pengembangan machine learning, tepatnya neural network yang merupakan implementasi dari metode deep learning. Secara umum model berbasis deep learning mampu mengekstrak pola dari hampir semua jenis data dan memberikan kita akses ke berbagai jenis model cerdas yang revolusioner.
Pada kaca mata sains dan akademik, pendekatan metode deep learning merupakan salah satu favorit karena alasan yang tersebut. Proses pemodelan bisa dilakukan dengan cepat, bisa menghasilkan akurasi yang baik, dan secara relatif proses pemodelan dapat dilakukan dengan sangat mudah.
Tetapi apakah pendekatan deep learning ini merupakan silver bullet yang bisa dipakai untuk segala jenis masalah pemodelan?🤔
Apa itu Deep Learning❓
Istilah deep learning sering kali digunakan secara sinonim untuk istilah neural network, padahal ada sedikit perbedaan diantara keduanya. Sebelum itu, kita perlu tau apa pengertian dari kedua istilah tersebut.
Kita akan mulai dari istilah neural network. Neural network merupakan pendekatan machine learning menggunakan konsep hubungan jaringan syaraf manusia, sedangkan deep learning merupakan model yang terdiri atas lapisan-lapisan neural network sehingga membentuk jaringan yang lebih kompleks (“dalam” atau deep).
Lalu bagaimana sebuah neural network bisa menghasilkan model dari data? Secara umum ada beberapa tahapan yang dilakukan pada sebuah neural network,
Ini adalah simplifikasi dan tidak akurat untuk menjelaskan neural network secara keseluruhan, lihat bagian Referensi untuk informasi lebih komprehensif
- Diberikan input data $X$ dengan target variabel $Y$ dan suatu jaringan yang merupakan kombinasi fungsi nonlinear $F(X) = \theta (W \cdot X + B)$ (disebut perceptron). Dimana $\theta$ adalah fungsi aktivasi (misalnya ReLU), $W$ adalah weights, dan $B$ adalah bias
- Hitung output prediksi $\hat{Y}=F(X)$, kemudian hitung loss atau cost $L = \mathcal{L}(Y, \hat{Y})$ misalnya menggunakan fungsi mean squared error
- Minimumkan fungsi $\mathcal{L}$, sehingga didapatkan suatu $\nabla W$ dan $\nabla B$ untuk mengubah nilai parameter awal sehingga $\hat{Y}$ mendekati $Y$
Sumber: Wikimedia Commons
Bisa disimpulkan, inti dari algoritma neural network adalah melakukan optimasi suatu fungsi $\mathcal{L}$ untuk mendapatkan nilai $W$ dan $B$ yang optimal sehingga output prediksi $\hat{Y}$ dapat mendekati $Y$. Sama seperti model regresi linier sederhana $y = ax + b$ kita harus mencari nilai $a$ dan $b$ untuk meminimumkan sum squared of errors, pada neural network kita ingin meminimumkan loss function untuk mendapatkan model terbaik. Perlu diketahui proses optimasi loss function biasanya dilakukan menggunakan metode gradient descent karena metode ini sangat efektif untuk dapat mengoptimasi fungsi yang memiliki banyak parameter.
Penulis merekomendasikan seri video dari 3Blue1Brown [1] untuk mempelajari lebih lanjut mengenai bagaimana neural network bekerja dari prespektif matematika.
Karena model berbasis neural network menggunakan kombinasi fungsi nonlinear dan memiliki parameter yang sangat banyak, model yang dihasilkan mampu mengekstrak hampir segala jenis pola dari dalam data. Inilah ide dari neural network, membuat model dengan jumlah parameter yang banyak dan input data yang besar, pola apapun akan bisa dimodelkan.
Tapi apa benar bisa begitu?
Data-driven vs Model-driven
Sumber: Matt W Newman dari Unsplash
Kita mungkin sudah sangat familiar dengan istilah model-driven, yaitu pemodelan yang dilakukan berdasarkan model yang sudah diciptakan sebelumnya, misalnya model regresi linier bivariat, model kuadratik, model logistic regression, dan banyak jenis model lainnya. Secara umum model-model ini menjelaskan hubungan antara variabel independen dan variabel dependen dalam suatu fungsi yang sudah pakem, yang perlu kita lakukan adalah mencari parameter terbaik berdasarkan data input. Biasanya metode yang digunakan untuk mencari parameter terbaik tadi dilakukan menggunakan metode least squares.
Pada model berbasis data-driven, model dibuat berdasarkan pola pada data dan tidak ada pakem tertentu. Misalnya pada model neural network, kita hanya perlu membuat network dengan jumlah perceptron secara arbiter dan kita bisa langsung memodelkan data kita. Bagaimana struktur model tidak dibatasi karena model akhir akan bergantung pada input data. Selain itu metode yang biasanya digunakan adalah optimasi metode numerik seperti L-BFGS dan gradient descent.
Pendekatan statistika, matematika, dan fisika biasanya menggunakan pendekatan model-based, di mana semua parameter dapat dikuantifikasi dan dapat diukur kontribusinya terhadap keseluruhan output. Selain itu pendekatan model-based juga tidak selalu mudah untuk dapat mencocokan dengan pola data input dan perlu untuk memenuhi berbagai asumsi dan sering kali diperlukan berbagai macam transformasi data agar model dapat mengeneralisasi pola pada data input. Berbeda dengan pendekatan machine learning di mana jumlah parameter dan bagaimana model dapat dibentuk sangat bergantung pada input data, sehingga sering kali model yang dihasilkan sulit untuk diinterpretasi tetapi memiliki kemampuan untuk mengeneralisasi data apapun.
Physics-informed Neural Networks (PINNs) 🧠
Seperti yang sudah dijelaskan pada bagian sebelumnya, pendekatan model-driven memiliki kelebihan bahwa model yang dibuat bisa didasarkan pada representasi dunia nyata, khususnya pada formulasi fisika, sedangkan pendekatan data-driven memiliki keunggulan bahwa model dapat dibuat dengan mengeneralisasi pola apapun dari input data, jika diberikan cukup banyak parameter.
Lalu bagaimana hubungan antara pendekatan model-driven dan data-driven?
Pada model fisika, kita memiliki banyak model untuk menjelaskan bagaimana fenomena di dunia terjadi, seperti bagaimana gerak benda-benda dan planet dapat dijelaskan oleh hukum Newton dan pompa hidrolik dapat dijelaskan oleh hukum Pascal. Tentunya kedua model ini mudah untuk dicari parameternya untuk menjelaskan suatu fenomena fisika. Masalah pemodelan fisika mulai menjadi menarik ketika kita ingin melakukan simulasi menggunakan model yang memiliki banyak parameter seperti persamaan Navier-Stokes yaitu persamaan yang menjelaskan mekanika fluida atau persamaan fungsi gelombang seperti persamaan Schrödinger yang menjelaskan posisi dan energi suatu elektron di dalam sebuah atom.
Sumber: Ivana Cajina dari Unsplash
Pendekatan yang umum digunakan untuk menyelesaikan model fisika tadi yang merupakan persamaan turunan parsial (PDE/partial derivative equations) [2] adalah dengan menggunakan metode numerik, salah satunya adalah metode finite element method (FEM). Jika teman-teman pernah menggunakan aplikasi simulasi seperti Ansys, SolidWorks, SimScale, atau aplikasi simulasi lain, kemungkinan besar metode FEM adalah metode yang digunakan oleh simulator tersebut.
Salah satu tantangan ketika menggunakan metode FEM adalah computational cost yang tinggi ketika mensimulasikan model dengan dimensi tinggi atau jumlah mesh yang banyak. Di sisi lain, neural network memiliki keunggulan karena implementasinya yang sebagian besar menggunakan autodifferentiation sehingga model dengan dimensi tinggi biasanya tidak menjadi masalah.
Berdasarkan alasan tersebut, mulai muncul pendekatan penyelesaian PDE menggunakan neural network. Ide penggunaan neural network sebagai metode penyelesaian atau aproksimator fungsi sudah ada sejak 1989 [3], tetapi pada tahun 2019 [4] implementasi neural network untuk menyelsaikan masalah PDE mulai menarik perhatian khususnya PDE pada model fisika. Pada tahun 2021 istilah physics-informed neural network digunakan untuk menjelaskan pemodelan fisika menggunakan pendekatan neural network [5, 6].
Menggabungkan Data dan Model
Seperti yang kita tahu, suatu neural network bekerja dengan cara meminimumkan suatu loss function $\mathcal{L}$ dengan cara melakukan gradient descent untuk mengestimasi parameter-parameter $W$ dan $B$. Secara umum, perubahan parameter-parameter tersebut didasarkan pada kemiripan antara output prediksi dan target nilai sebenarnya $\mathcal{L}(\hat{Y}, Y)$, semakin kecil loss, maka semakin akurat model neural network tersebut.
Karena perubahan parameter-parameter tersebut diarahkan oleh turunan dari loss function (berupa gradient), kita bisa menyisipkan model fisika sebagai bagian dari loss function untuk mengarahkan bagaimana neural network dapat mengeneralisasi parameter-parameternya.
Jika pada neural network kita hanya memiliki satu loss function,
$$ L = \mathcal{L}(\hat{Y}, Y) $$
Pada PINN kita menambahkan PDE yang akan diaproksimasi $g(X, \hat{Y})$ pada loss function,
$$ L_{total} =\mathcal{L}(\hat{Y}, Y) + g(X, \hat{Y}) $$
sehingga pada setiap iterasi gradient descent, parameter-parameter pada physics loss $g(X, \hat{Y})$ dapat diminimumkan, menghasilkan model yang memiliki sifat yang sama seperti model fisika $g$.
Inilah kunci dari PINN, kita ingin membuat model neural network yang mematuhi aturan model fisika dengan cara mengarahkan model dengan menggunakan PDE sebaai loss function.
Pada bagian conton implementasi, kita akan lihat bagaimana perbedaan model neural network biasa dibandingkan dengan PINN dapat digunakan untuk menyelesaikan dua masalah fisika sederhana.
Implementasi PyTorch🔥
Source code bisa diakses melalui Google Colab dengan klik tombol di bagian awal artikel
Penulis tidak akan memberikan pendahuluan mengenai PyTorch, teman-teman bisa mencari sendiri referensi mengenai PyTorch!
Ketika kita membuat model neural network, tentunya kita perlu membuat struktur jaringannya terlebih dahulu dengan cara membuat kelas baru dari nn.Module, misalnya:
class NeuralNetwork(nn.Module):
def __init__(self):
super().__init__()
self.fcn = nn.Sequential(
nn.Linear(28*28, 512),
nn.ReLU(),
nn.Linear(512, 512),
nn.ReLU(),
nn.Linear(512, 10)
)
def forward(self, x):
logits = self.fcn(x)
return logits
Proses yang menarik dari implementasi PINN ini terjadi pada tahap training, karena kita harus membuat sendiri fungsi fit untuk menghitung kedua loss function. Secara umum proses training dapat dijabarkan sebagai berikut.
# konversi input data sebagai tensor
Xt = np_to_torch(X)
yt = np_to_torch(y)
# membuat optimizer, misalnya Adam
optimizer = torch.optim.Adam(self.parameters(), lr=self.lr)
# mulai proses training
self.train()
for i in range(self.epochs):
# membuat gradient menjadi nol
optimizer.zero_grad()
# menghitung "data loss"
outputs = self.forward(Xt)
loss = self.data_loss(yt, outputs)
# menghitung "physics loss"
if self.physics_loss:
loss += self.physics_loss_weight * self.physics_loss(self)
# lakukan backpropagation
loss.backward()
optimizer.step()
data_loss merupakan variabel yang merujuk pada loss function klasik seperti mean squared error untuk menghitung loss antara data prediksi dan data target. Hal yang menarik terjadi pada variabel physics_loss yang merupakan loss function untuk mengkuantifikasi loss berdasarkan model fisika.
Kita akan lihat dua contoh penerapan PINN pada dua model fisika sederhana, yaitu hukum pendinginan Newton dan hukum gerak Newton mengenai gerak harmonik.
Hukum Pendinginan Newton❄️
Implementasi PINN yang pertama akan kita bahas adalah mengenai hukum pendinginan Newton yang terinspirasi dari [7]. Hukum pendinginan Newton berbunnyi:
The rate of heat loss of a body is directly proportional to the difference in the temperatures between the body and its environment.
Sumber: Clay Banks dari Unsplash
Misalnya kita membuat kopi☕ dengan air mendidih bersuhu 90 °C kemudian kita tinggalkan di ruangan bersuhu 25 °C. Hukum Newton menyatakan bahwa laju pendinginan akan proposional antara suhu lingkungan dan suhu kopi yang dapat dinotasikan:
$$ \begin{aligned} \dot{Q} &= hA(T(t) - T_{env}) \\ &= hA \Delta T(t) \end{aligned} $$
Dengan menurunkan persamaan di atas terhadap waktu, kita bisa mendapatkan fungsi suhu terhadap waktu,
$$ \frac{\mathrm{d}T(t)}{\mathrm{d}t} = R(T_{env} - T(t)) $$
dengan solusi analitik [8],
$$ T(t)=T_{\text{env}}+(T(0)-T_{\text{env}})e^{-rt}. $$
Nah berdasarkan persamaan di atas, kita tahu bahwa seberapa cepat suhu kopi berubah mendekati ekuilibrium dengan suhu ruangan dipengaruhi oleh suatu konstanta $R$ (konstanta tingkat laju pendinginan), semakin besar nilai $R$ maka semakin cepat pula suhu kopi akan mencapai ekuilibrium.
Tentu kita bisa menyelesaikan masalah di atas dengan metode analitik dengan mudah karena hanya terdapat dua konstanta dan satu variabel. Tapi ingat, ide dari PINN adalah menyelesaikan PDE yang memiliki banyak koefisien sehingga contoh ini hanyalah gambaran saja!
Membangkitkan Dataset
Tahap awal dari semua jenis pemodelan dengan neural network adalah membangkitkan data. Pada kasus ini kita akan menggunakan beberapa parameter awal sebagai berikut.
def cooling_analytic(Tenv, T0, R, x):
return Tenv + (T0 - Tenv) * np.exp(-R * x)
# konstanta pendingingan
Tenv = 25 # suhu lingkungan
T0 = 100 # suhu awal
R = 0.005 # cooling rate
# menghitung perubahan suhu menggunakan solusi analitik
X = np.linspace(0, 1000, 1000).reshape(-1, 1)
y = cooling_analytic(Tenv, T0, R, X).reshape(-1, 1)
# ambil sebagian titik data untuk data latih/training ditambah gaussian noise
# pada dunia nyata, data ini merupakan data pengamatan/laboratorium
X_train, y_train = split_train(X, y, max=400, step=20, noise=True, mean=0.0, scale=1.0)
print(X_train.shape, y_train.shape)
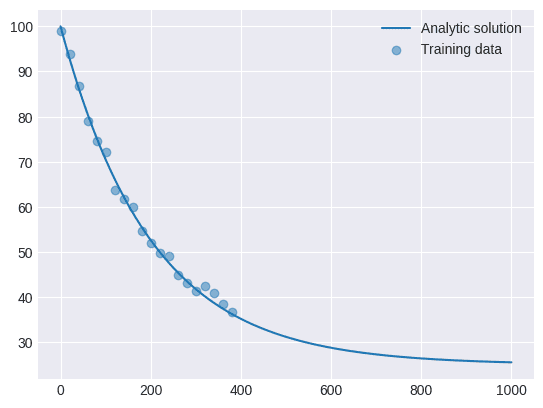
Sumber: Penulis
Pada kasus ini penulis membangkitkan 1000 titik data waktu antara 0 s.d. 1, kemudian penulis mengambil 20 titik data (hanya 2% saja!) dari data awal sebagai data latih. Pada dunia nyata, data ini idealnya didapatkan dari sensor atau sistem yang ingin dimodelkan. Selain itu penulis juga menambahkan noise pada data training untuk memperlihatkan bagaimana PINN mampu mengeneralisasi model meskipun datanya memiliki noise.
Pada proses pemodelan, penulis melakukan pemodelan menggunakan neural network yang memiliki 3 hidden layer dengan 32 unit per layer dengan empat skenario, yaitu:
- neural network biasa (MLP)
- ditambah L2 regularization (L2 Reg),
- menggunakan PINN (PINN),
- dan PINN ditambah pencarian parameter (PINN v2).
Proses training dilakukan menggunakan optimizer Adam dengan learning rate = 0.0001 dan epochs = 20.000
Hasil dan Pembahasan
Terdapat lebih banyak grafik pada Google Colab😁
| Model | MSE | MAPE |
|---|---|---|
| MLP | 71.26 | 0.22 |
| L2 Reg | 913.28 | 0.78 |
| PINN | 1.92 | 0.03 |
| PINN v2 | 0.57 | 0.01 |
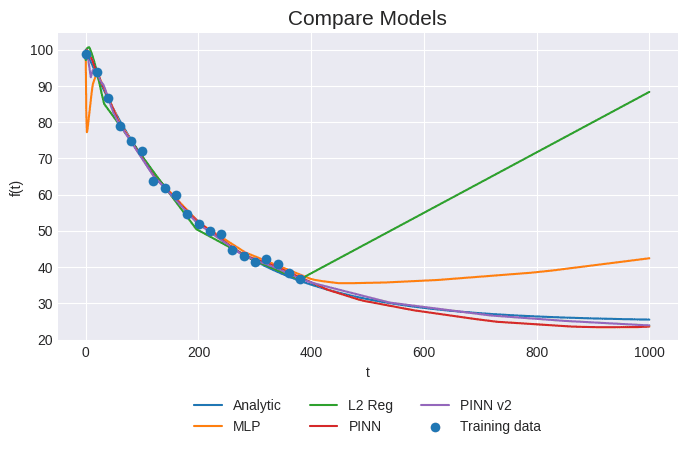
Pada grafik di atas kita bisa amati model MLP dan MLP+L2 Reg mampu mendekati arah pendinginan tapi terbatas pada sampel input data saja, ketika model diberikan data uji di luar dari domain data input, model MLP dan L2 Reg gagal memprediksi dengan akurat nilai $T$ yang sesungguhnya. Meskipun kita telah menggunakan metode L2 regularization yang biasa digunakan untuk mencegah overfitting, model tetap tidak bisa mengeneralisasi pola dari data dengan akurat. Inilah salah satu kelemahan dari data-driven modelling dan pendekatan neural network pada umumnya yaitu kita membutuhkan data dalam jumlah besar dan struktur jaringan yang cukup besar untuk dapat mengeneralisasi pola dari data.
Jika kita bandingkan dengan PINN dan PINN v2, kedua model ini mampu menghasilkan prediksi yang mendekati model analitik, artinya model ini lebih cocok untuk digunakan memprediksi sifat pendinginan objek karena mampu mengikuti hukum pendinginan Newton.
Estimasi Parameter R
Pada model PINN kita sudah tahu bahwa nilai $R = 0.005$ sedangkan pada model PINN v2 kita tidak memasukkan nilai $R$, melainkan kita membuat nilai R sebagai parameter yang akan dicari oleh PINN. Berdasarkan hasil training, didapatkan nilai $R = 0.0044$, tidak terlalu jauh berbeda dengan nilai $R$ sesungguhnya kan?
Jadi bisa disimpulkan dari eksperimen ini bahwa PINN selain mampu mengaproksimasi PDE tetapi bisa juga mengaproksimasi parameter-parameter dalam model PDE.
Gerak Harmonik Teredam🏀
Pada contoh kedua ini kita akan menggunakan hukum gerak Newton $F=ma$ dan hukum Hooke $F=-kx$, contoh ini juga terinspirasi dari [9, 10, 11]. Persamaan gerak yang ingin kita modelkan adalah persamaan gerak harmonik. Teman-teman pasti sudah pernah mempelajari ini di SMA dulu. Gerak harmonik sederhana adalah gerak bolak-balik benda melalui suatu titik kesetimbangan tertentu dengan banyaknya getaran benda dalam setiap sekon selalu konstan.
Misal kita punya sebuah pegas dengan massa yang tergantung di ujungnya, jika kita tarik pegas tersebut, maka pegas akan berosilasi.

Sumber: Svjo dari Wikimedia Commons
Jika kita mengabaikan gaya gesek dan hambatan udara, maka gerak tersebut akan terjadi terus menerus karena tidak ada perubahan total energi pada sistem, tetapi kondisi ini tentunya adalah kondisi ideal dan tidak mungkin terjadi di dunia nyata karena energi pasti akan hilang ke lingkungan karena hukum termodinamika.
Maka dari itu gerak harmonik yang menjadi fokus pembahasan kita adalah gerak harmonik teredam yang mana osilasi pada akhirnya akan berhenti karena hilangnya energi ke lingkungan.
Secara umum gerak harmonik dapat dituliskan sebagai berikut.
$$ m \dfrac{d^2 x}{d t^2} + \mu \dfrac{d x}{d t} + kx = 0, $$
Pada kasus gerak harmonik teredam, yang mana sistem berosilasi dengan amplitudo yang secara gradual mendekati nol, terdapat kondisi
$$ \delta < \omega_0, \qquad \text{dengan} \quad \delta = \dfrac{\mu}{2m}~,~\omega_0 = \sqrt{\dfrac{k}{m}}, $$
Gerak harmonik teredam memiliki solusi analitik:
$$ x(t) = e^{-\delta t}(2 A \cos(\phi + \omega t)), \qquad \mathrm{dengan} \quad \omega=\sqrt{\omega_0^2 - \delta^2} $$
Sekarang bayangkan kita mempunyai sistem yang sama dan ingin kita modelkan menggunakan PINN. Kita akan menggunakan skenario yang mirip seperti pada contoh sebelumnya tapi kita hanya akan menggunakan dua skenario yaitu MLP dan PINN.
Membangkitkan Dataset
Sama seperti sebelumnya kita akan membangkitkan data menggunakan pendekatan analitik.
def oscillator_analytic(d, w0, x):
assert d < w0
w = np.sqrt(w0**2-d**2)
phi = np.arctan(-d/w)
A = 1/(2*np.cos(phi))
return np.exp(-d*x)*2*A*np.cos(phi+w*x)
# konstanta osilasi
d = 2
w0 = 20
# membuat osilasi menggunakan solusi analitik
X = np.linspace(0, 1, 500).reshape(-1, 1)
y = oscillator_analytic(d, w0, X).reshape(-1, 1)
# ambil sebagian titik data untuk data latih/training
# pada dunia nyata, data ini merupakan data pengamatan/laboratorium
X_train, y_train = split_train(X, y, max=200, step=20, noise=False)
print(X_train.shape, y_train.shape)
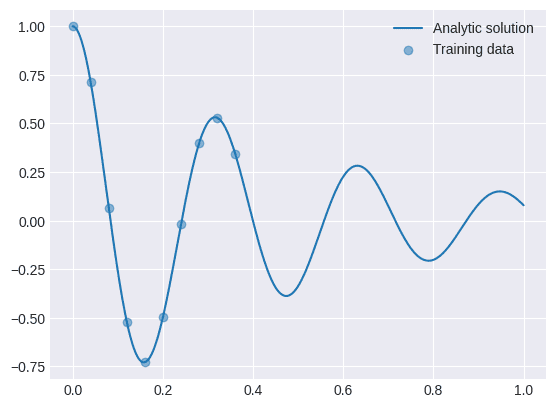
Sumber: Penulis
Jika kita perhatikan pada kasus ini data yang dibuat tidak turun secara polinomial, melainkan dataset ini berupa gelombang sinus yang terus mendekati nol. Bagaimana efek dari gelombang periodik ini terhadap prediksi model?
Hasil dan Pembahasan
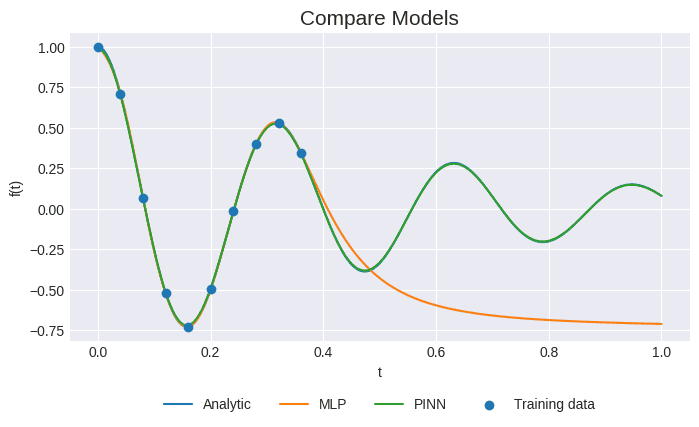
Sumber: Penulis
| Model | MSE | MAPE |
|---|---|---|
| MLP | 0.24 | 18.13 |
| PINN | 0.00 | 0.02 |
Berdasarkan grafik prediksi dapat dilihat bahwa model MLP tidak mampu mengeneralisasi sifat periodik dari data tetapi model PINN mampu mengeneralisasi data dengan baik. Berdasarkan eksperimen kedua ini kita bisa simpulkan bahwa model PINN mampu mengeneralisasi model yang tidak hanya bersifat polinomial tetapi juga bersifat gelombang/periodik.
Teman-teman mungkin penasaran bagaimana proses training PINN ini berlangsung, berikut adalah visualisasi proses training selama 20.000 epochs. Perhatikan bagaimana pada awal proses training output dari model adalah konstan dan mulai bergeser mendekati fungsi PDE yang dimasukkan pada loss function.
Simpulan💡
Menarik sekali ya teman-teman bagaimana neural network bisa kita manfaatkan untuk memodelkan sistem fisika. Berangkat dari ide bahwa neural network mampu mengekstrak pola dari data apapun jika diberikan cukup banyak parameter, ide ini dikembangkan untuk menggunakan neural network dalam penyelesaian masalah persamaan turunan parsial (PDE). Karena kemampuannya yang universal untuk menyelesaikan PDE, berbagai model fisika mulai diterapkan menggunakan neural network untuk menciptakan model yang dapat dibuat dengan data observasi yang sedikit tetapi mampu mengikuti aturan fisika.
Dari beberapa eksperimen yang sudah kita lakukan, ada beberapa hal yang bisa kita amati,
- Neural network dapat digunakan untuk menyelesaikan PDE permasalahan fisika
- Neural network mampu mengeneralisasi model dengan bantuan PDE pada loss function, menghasilkan PINN
- PINN membutuhkan sedikit data observasi untuk dapat mengeneralisasi model, tetapi datanya harus representatif dan terbebas (atau sedikit) dari noise
- PINN mampu melakukan pencarian parameter pada PDE
- PINN membutuhkan waktu training yang lama (epoch yang besar)
Nah dari banyaknya kelebihan PINN ini, beberapa penelitian saat ini sedang melihat kemungkinan implementasi PINN sebagai digital twin [12]. Digital twin merupakan model komputer dari alat fisik atau sistem yang merepresentasikan semua sifat fisik sistem dan hubungannya. Dengan kata lain kita bisa memiliki versi digital dari suatu alat atau sistem fisik. Bayangkan kita punya sebuah akuarium, dengan digital twin kita bisa tahu persis bagaimana pertumbuhan lumut, perubahan zat-zat terlarut dalam air, dan lainnya dalam versi digital sehingga kita bisa melakukan simulasi atau prediksi sebelum kita melakukan aksi nyata. Proses prediksi ini sangat penting khususnya di industri di mana banyak sistem-sistem penting yang perlu dijaga keberlangsungan operasinya.
Sampai di sini dulu artikel kali ini dan artikel ini juga merupakan artikel terakhir penulis di tahun 2023.
Kita akan ketemu lagi di tahun depan dengan lebih banyak konten mengenai data mining dan web scraping.
Stay tuned!
Referensi📚
- But what is a neural network? | Chapter 1, Deep learning. Diakses: 22 Desember 2023. [Daring Video]. Tersedia pada: https://www.youtube.com/watch?v=aircAruvnKk&list=PLZHQObOWTQDNU6R1_67000Dx_ZCJB-3pi
- “Partial differential equation,” Wikipedia. 28 November 2023. Diakses: 20 Desember 2023. [Daring]. Tersedia pada: https://en.wikipedia.org/Partial_differential_equation
- K. Hornik, M. Stinchcombe, dan H. White, “Multilayer feedforward networks are universal approximators,” Neural Networks, vol. 2, no. 5, hlm. 359–366, Jan 1989, doi: 10.1016/0893-6080(89)90020-8.
- M. Raissi, P. Perdikaris, dan G. E. Karniadakis, “Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations,” Journal of Computational Physics, vol. 378, hlm. 686–707, Feb 2019, doi: 10.1016/j.jcp.2018.10.045.
- G. E. Karniadakis, I. G. Kevrekidis, L. Lu, P. Perdikaris, S. Wang, dan L. Yang, “Physics-informed machine learning,” Nat Rev Phys, vol. 3, no. 6, hlm. 422–440, Jun 2021, doi: 10.1038/s42254-021-00314-5.
- S. Lee, “Physics-informed Neural Networks (PINN).” Diakses: 20 Desember 2023. [Daring]. Tersedia pada: https://i-systems.github.io/tutorial/KSNVE/220525/01_PINN.html
- T. Wolf, “Physics-informed Neural Networks: a simple tutorial with PyTorch,” Medium. Diakses: 23 Desember 2023. [Daring]. Tersedia pada: https://medium.com/@theo.wolf/physics-informed-neural-networks-a-simple-tutorial-with-pytorch-f28a890b874a
- S. Maruyama dan S. Moriya, “Newton’s Law of Cooling: Follow up and exploration,” International Journal of Heat and Mass Transfer, vol. 164, hlm. 120544, Jan 2021, doi: 10.1016/j.ijheatmasstransfer.2020.120544.
- B. Moseley, “So, what is a physics-informed neural network?” Diakses: 20 Desember 2023. [Daring]. Tersedia pada: https://benmoseley.blog/my-research/so-what-is-a-physics-informed-neural-network/
- T. P. Negara dan A. Ismangil, Metode numerik, 1 ed. Bogor: Universitas Pakuan Press, 2017.
- I. Berg, “Damped Harmonic Oscillator - Derivation and solution of the differential equations.” Diakses: 20 Desember 2023. [Daring]. Tersedia pada: https://beltoforion.de/en/harmonic_oscillator/
- A. Fuller, Z. Fan, C. Day, dan C. Barlow, “Digital twin: enabling technologies, challenges and open research,” IEEE Access, vol. 8, hlm. 108952–108971, 2020, doi: 10.1109/ACCESS.2020.2998358.
- T. G. Grossmann, U. J. Komorowska, J. Latz, dan C.-B. Schönlieb, “Can Physics-Informed Neural Networks beat the Finite Element Method?,” arXiv.org. Diakses: 23 Desember 2023. [Daring]. Tersedia pada: https://arxiv.org/abs/2302.04107v1


